Skewness[ˋskjunɪs] 稱為偏度,這是分析離群值的重要演算法,屬於特徵工程的一種。就是在眾多的特徵中,將有問題特徵挑出來,再進行後續的處理。後續怎麼處理呢? 方法可多著了,比如用 log 拉近,也可用平方根,三次方根,或者更絕的就是直接去除。
至於 Skewness 怎麼計算呢,請放慢腳步,看看底下的說明。
Seaborn位置分佈
上一章的 波士頓房價預測,可以看出 LSTAT 的值呈現如下分佈
import pandas as pd
import seaborn as sns
import pylab as plt
display=pd.options.display
display.max_columns=None
display.max_rows=None
display.width=None
display.max_colwidth=None
df=pd.read_excel("boston.xlsx", sheet_name='Sheet1',index_col=0, keep_default_na=False)
lstat=df['LSTAT']
skew=round(lstat.skew(),2)
sns.histplot(lstat, kde=True)
plt.title(f'skew:{skew}')
plt.show()
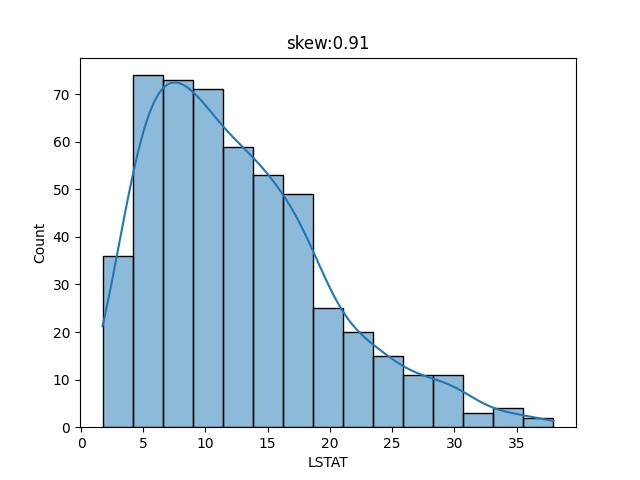
整個分佈圖中,窮人的比例大都集中在 10%~20% 左右,但有著極少的數量介於30%-36%之間,這些少數的數量就是所謂的離群值,也就是異常的地方。
上面的代碼中, lstat.skew()就是計算偏度值,其值為 0.91。此值正數表示整個分佈重心在邊左,然後向右邊有零星的異常值。負數表示重心在右邊,然後左邊有零星的異常值。當然最好的資料 skew 為0。
修正Skewness
理論上(假設) skew 值愈接近 0 ,讓整個重心愈靠近中心,所預測出來的值就會更準確。所以我們先修正skew, 再來驗証預測的分數是否會提高。
修正 skew 有許多方法,目前我們將 LSTAT 開立方根看看 skew 的值是否有接近 0
import pandas as pd
import seaborn as sns
import pylab as plt
display=pd.options.display
display.max_columns=None
display.max_rows=None
display.width=None
display.max_colwidth=None
df=pd.read_excel("boston.xlsx", sheet_name='Sheet1',index_col=0, keep_default_na=False)
lstat=df['LSTAT']**(1/3)
skew=round(lstat.skew(),2)
sns.histplot(lstat, kde=True)
plt.title(f'skew:{skew}')
plt.show()
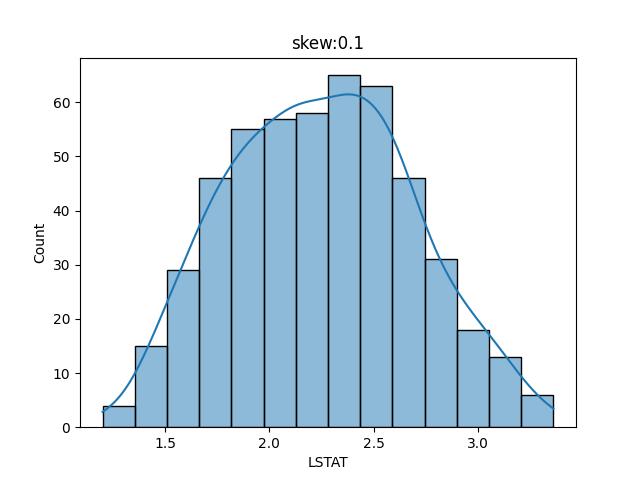
很明顯的,當 LSTAT 進行立方根後,skew 的值由 0.91 減到 0.1,整個重心就居於中心點了。
驗証
接下來就要驗証上一章節的房價預測了,當 LSTAT 的 skew減少後,預測的分數是否有提高。
import pandas as pd
import numpy as np
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
display=pd.options.display
display.max_columns=None
display.max_rows=None
display.width=None
display.max_colwidth=None
df=pd.read_excel("boston.xlsx", sheet_name='Sheet1',index_col=0, keep_default_na=False)
lstat=df['LSTAT']**(1/3)
data=np.c_[lstat, df['RM']]
x=pd.DataFrame(data=data, columns=['LSTAT','RM'])
y=df['PRICE']
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size = 0.2, random_state=5)
model=LinearRegression()
model.fit(x_train, y_train)
print(f'score:{model.score(x_test, y_test)}')#由0.66變成了 0.71
y_pred=model.predict(x_test)
for i in zip(y_pred, y_test):
print(i)
結果:
score:0.7130425972530741
(39.22636905921109, 37.6)
(31.439969891896475, 27.9)
(25.414952092316256, 22.6)
(3.9262874226402076, 13.8)
(32.44566540604957, 35.2)
(9.066374212216349, 10.4)
(31.224813886303775, 23.9)
(27.3198146314941, 29.0)
結果的確讓人驚訝,預測分數由 0.66 提升到了 0.71,所以會讓我們更相信預測出來的房價會更加的準確??
這是因為LTAT 是負相關,所以要開根才會讓重心移到中心。
繼續修正RM值
RM值就是每間房子的房間數,當然是房間數愈多會愈貴,是吧。但當中也有許多異常點,所以繼續作修正。
import pandas as pd
import numpy as np
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
display=pd.options.display
display.max_columns=None
display.max_rows=None
display.width=None
display.max_colwidth=None
df=pd.read_excel("boston.xlsx", sheet_name='Sheet1',index_col=0, keep_default_na=False)
lstat=df['LSTAT']**(1/3)
rm=df['RM']**(1/3) #預測分數減少到 0.69
#rm=df['RM']**2 # 預測分數又提高到 0.74
#data=np.c_[lstat, df['RM']]
data=np.c_[lstat, rm]
x=pd.DataFrame(data=data, columns=['LSTAT','RM'])
y=df['PRICE']
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size = 0.2, random_state=5)
model=LinearRegression()
model.fit(x_train, y_train)
print(f'score:{model.score(x_test, y_test)}')#由0.66變成了 0.71
y_pred=model.predict(x_test)
for i in zip(y_pred, y_test):
print(i)
結果:
score:0.6933638393907695
(38.45538047968539, 37.6)
(31.611331631812117, 27.9)
(25.513028183308485, 22.6)
(3.7861411792769664, 13.8)
(31.78366118039205, 35.2)
(9.059471878964969, 10.4)
(31.13806230021166, 23.9)
很奇怪的是,上述紅色的代碼,當 RM 使用立方根讓 skew 減少並接近 0 時,預測的分數減少到 0.69,反正不準。但如果將 RM 使用平方讓 skew 加大,分數反而增加到 0.74。
這是為什麼呢? 因為 RM 是房間數愈多愈貴,是正相關,所以當然要平方才會將重心拉到中間。
結論
每次都聽人家說,必需調整參數,到底是在調什麼? 上述的 LSTAT 立方根,或是 RM 的平方,甚至是加入其它的特徵,都會影響預測的值。畢竟房價不像用斤兩來秤有絕對的標準,更何況房價還要依賣方的心情,當前的通膨,人均所得,根本就沒有標準。人量不出來的,更別想叫電腦算的準。
不論國內或國外,房仲都是一個很黑的行業,會根據他們所購入的價格,調整一個可以讓他們獲得最大利益的參數或模型,也讓無知的百姓誤以為他們是公平公正有絕對的公式來計價。別傻了,就算你把這些仲介的祖宗18代都挖出來,他們還是不會把這些參數及模型公佈出來。
不過,我們自已調整及建立的模型,將 score 調到最高,雖說還是不準確,但絕對是值得參考的依據。
