學習率的問題
學習率的大小對梯度下降的搜索過程影響非常大,太小搜索速度慢,太大又可能跳過極值。上述手動選擇學習率的方式,稱為SGD 隨機梯度下降法,每次的學習率都是固定的。手動選擇適當的學習率往往要花費不少時間,所以可以用如下三種方式自動幫我們選擇學習率
1. 衰減因子
2. 引入動量
3. 自動調整學習率(自適應梯度策略,又稱為優化器 Optimizer)
學習率衰減因子
把初始學習率預設為 1,然後依迭代的次數,逐步減少。迭代公式如下
$(lr_{i} = \frac{lr_{0}}{(1.0 + decay * i)})$
$(lr_{0})$ 為初始學習率,decay 為衰減因子,i 為第 i 次迭代,$(lr_{i})$ 為第 i 次迭代所計算出來的學習率。
衰減因子愈小,衰減率會愈大,就會更快接近極值。但此時的初始學習率亦必需設定大一點,如果初始學習率設太小,衰減愈不明顯。底下是 Python 完整代碼
#衰退因子 : 一開始比較快,後面愈來愈慢
import numpy as np
import pylab as plt
def f(x):
return np.square(x)
def df(x):
return 2 * x
def bias(a, x):
b=f(x)- a * x
return b
x=np.linspace(-5, 5, 100)
y=f(x)
current_x=-5
traces=[current_x]
epochs=500
lr=0.2
decay = 0.1
fig=plt.figure(figsize=(9,6))
ax=plt.axes()
for i in range(epochs):
ax.clear()
ax.set_xlim(-10,10)
ax.set_ylim(-5,30)
plt.plot(x,y)
plt.scatter(traces, f(traces), c='r')
a=df(current_x)
b=bias(a, current_x)
x_l=current_x-3
x_r=current_x+3
line_x=[x_l, x_r]
line_y=[a*(x_l)+b, a*(x_r)+b]
plt.plot(line_x, line_y, c='orange')
#基本
#current_x = current_x - a * lr
#衰減因子
lr_i = lr / (1 + decay * i)
current_x = current_x - a * lr_i
traces.append(current_x)
plt.pause(0.01)
plt.show()
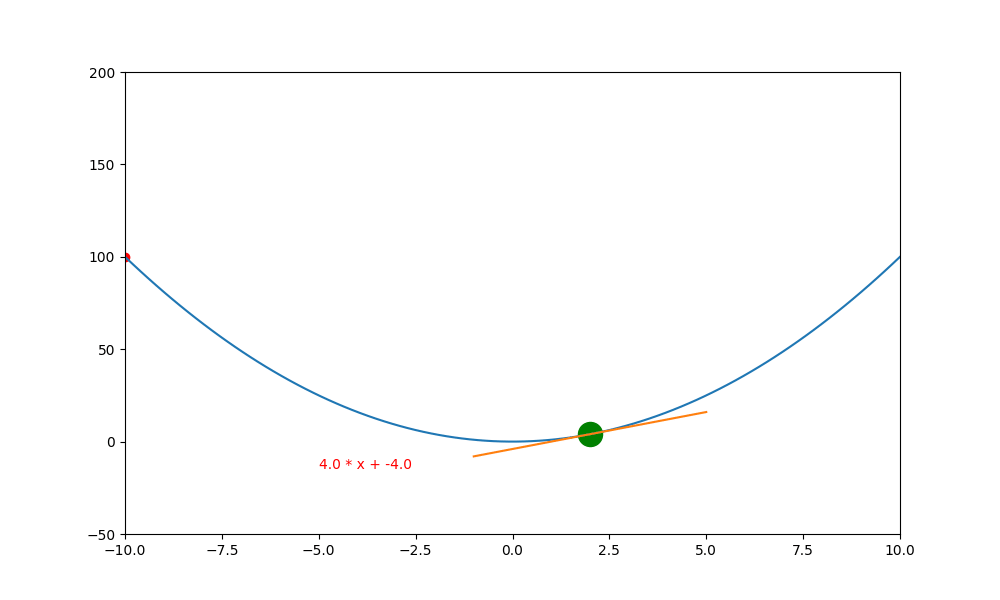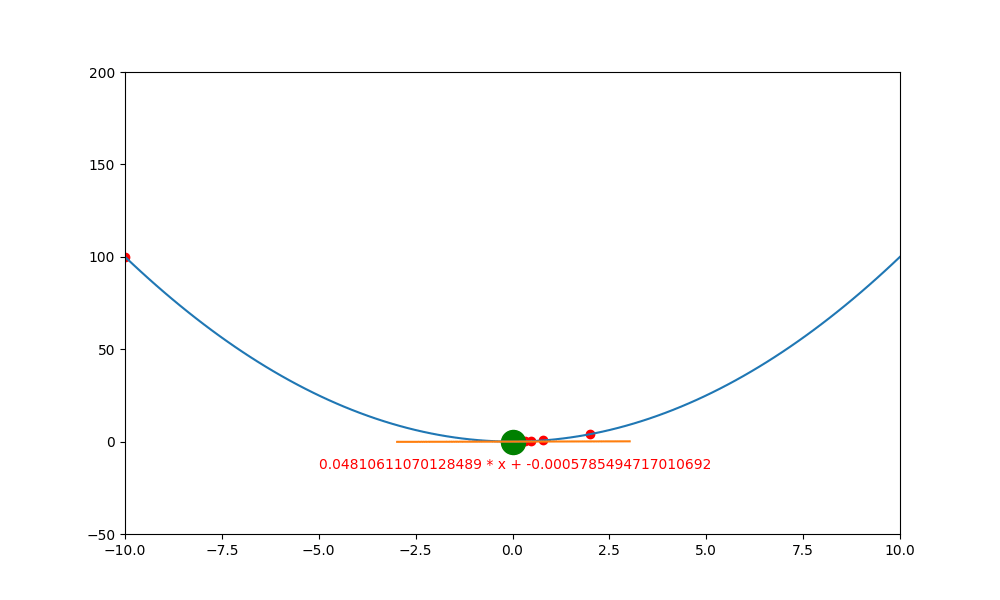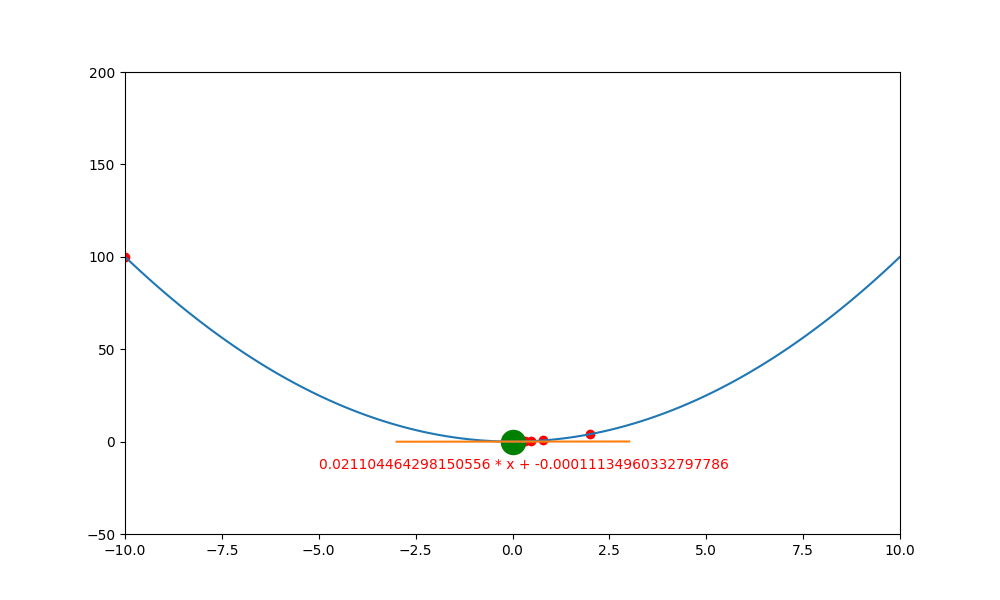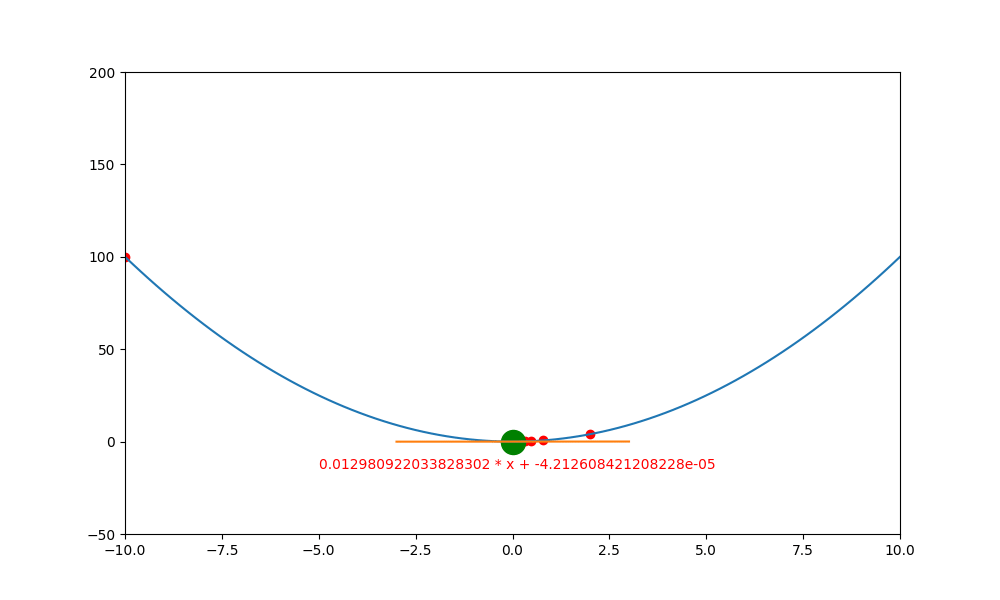
底下是初始學習率 0.4 ,decay 為 0.99 所執行的圖解。
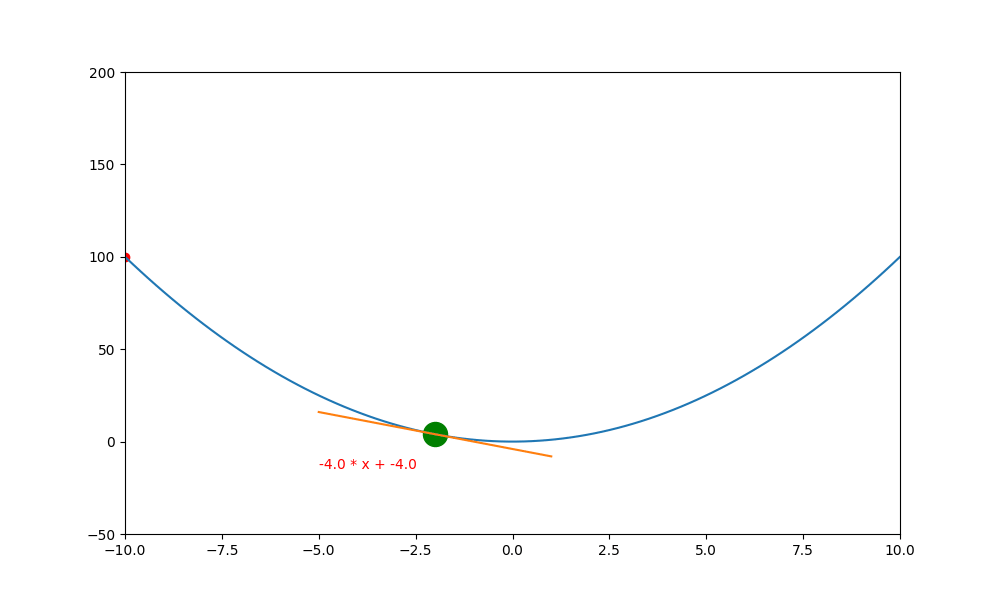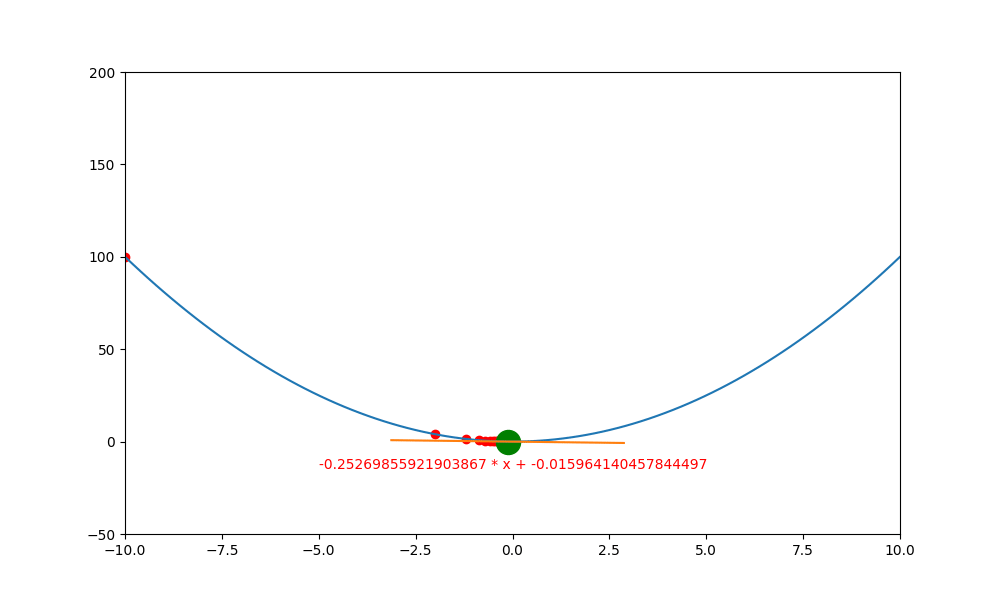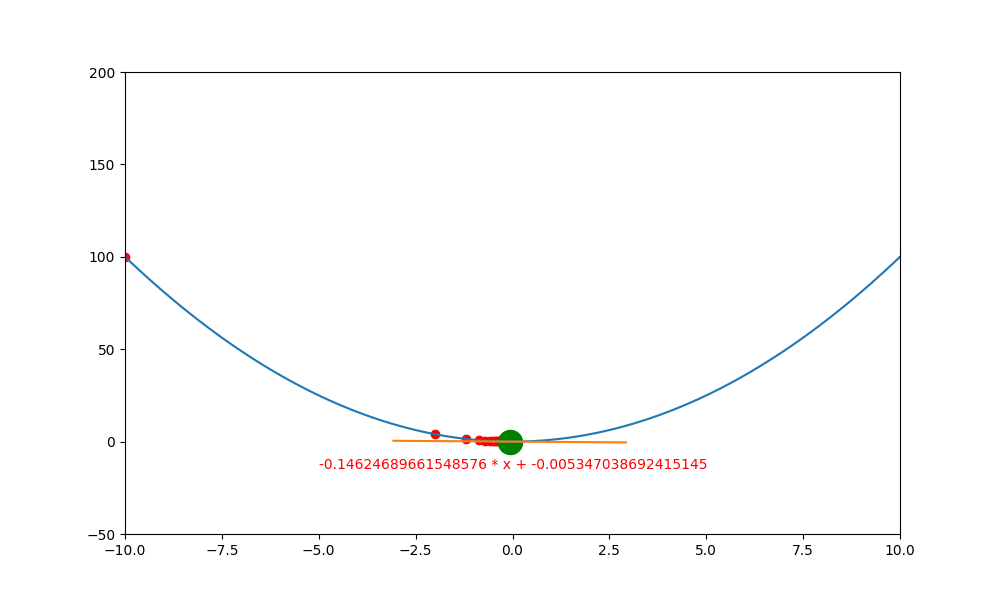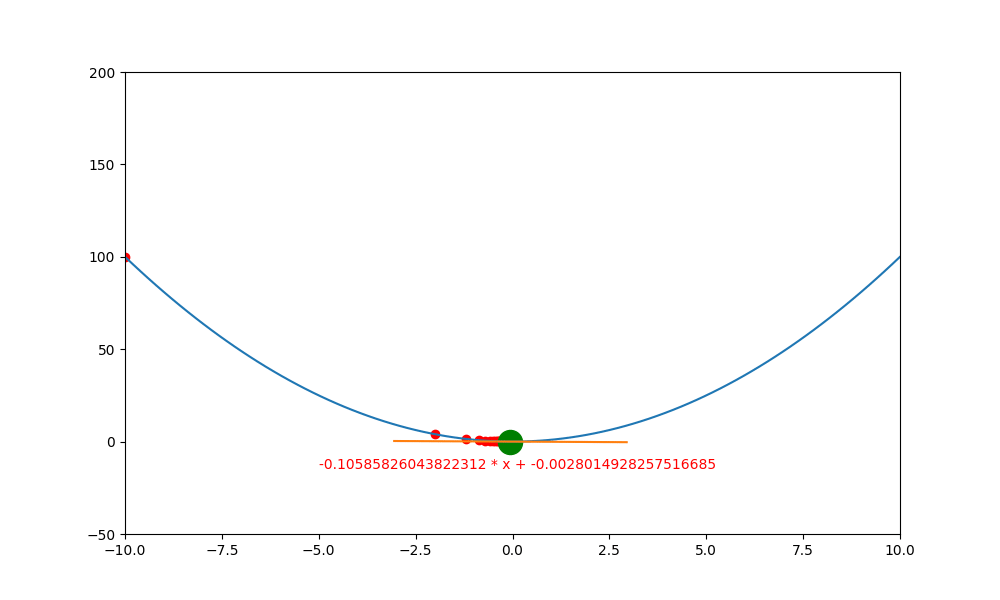
底下是初始學習率 0.6 ,decay 為 0.99 所執行的圖解, 一下就找到極值。如果初始學習率設定為 0.5 ,則會更快,馬上就不動了
引入動量
物理學的動量定義為 質量 * 速度,也就是 m * v。當 m 為一單位質量時,v 就是動量。一開始設定 v = 0 (一開始不動),然後每次迭代 v = -a * lr + mu * v ,mu 是要縮小動量的小參數。底下是 Python 代碼。
import numpy as np
import matplotlib.pyplot as plt
#目標函數 y=x^2
def f(x):
return np.square(x)+2
#目標函數的一階導數 dy/dx=2*x
def df(x):
return 2 * x
def bias(a,x):
b=f(x) - a * x
return b
plt.figure(figsize=(9,6))
epochs = 100
lr = 0.2
ax=plt.axes()
x = np.linspace(-5, 5, 100)
current_x=-5
y=f(x)
traces=[current_x]
v=0
mu = 0.9
for i in range(epochs):
ax.clear()
ax.set_xlim(-10,10)
ax.set_ylim(-3, 35)
ax.plot(x, y)
#對目標函數進行微分
a=df(current_x)
b=bias(a, current_x)
#畫導線
xl=current_x-3
xr=current_x+3
yl = a * xl + b
yr = a * xr + b
ax.plot([xl, xr], [yl, yr], c='orange')
ax.scatter(traces, f(traces), s=10, c='r')
ax.scatter(current_x, f(current_x), c='g', s=200)
ax.text(-2,-15, f'{a:.7f} * x + {b:.7f}', color='red')
# 計算動量
v = a * lr + mu * v
# 計算下一步 (x,y)
current_x -= v
traces.append(current_x)
plt.pause(0.1)
plt.show()
下圖是執行後的結果,可以看到就好像一顆圓球,滑入一個凹槽中,然後來回左右滾動。所以如果想要製作這種模擬現實生活中滾來滾去的動畫,加入動量是最好的方法。
動量的作用,其實就是在平滑之處,有鼓力量將現在的位置往前推(慣性),讓它越過目前的門檻。當然啦,如果動量不足以跨不出目前的門檻,還是會被打回而卡住。
所以引入動量的方法,只是去探測未來的高度是否還是跟往惜一樣的平坦,用此動能衝看看,如果可以跨過就往前,如果跨不過去就反彈。
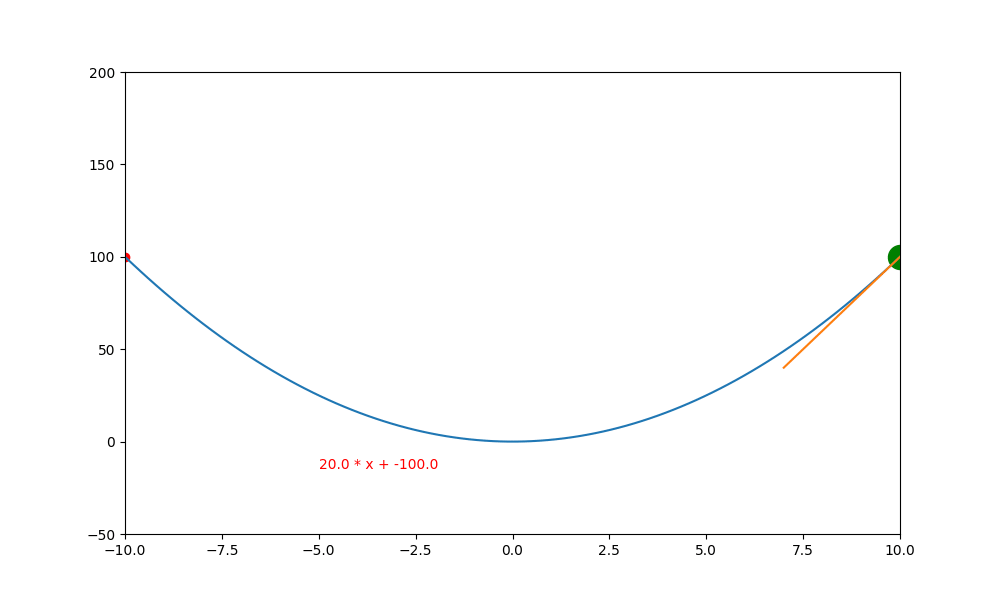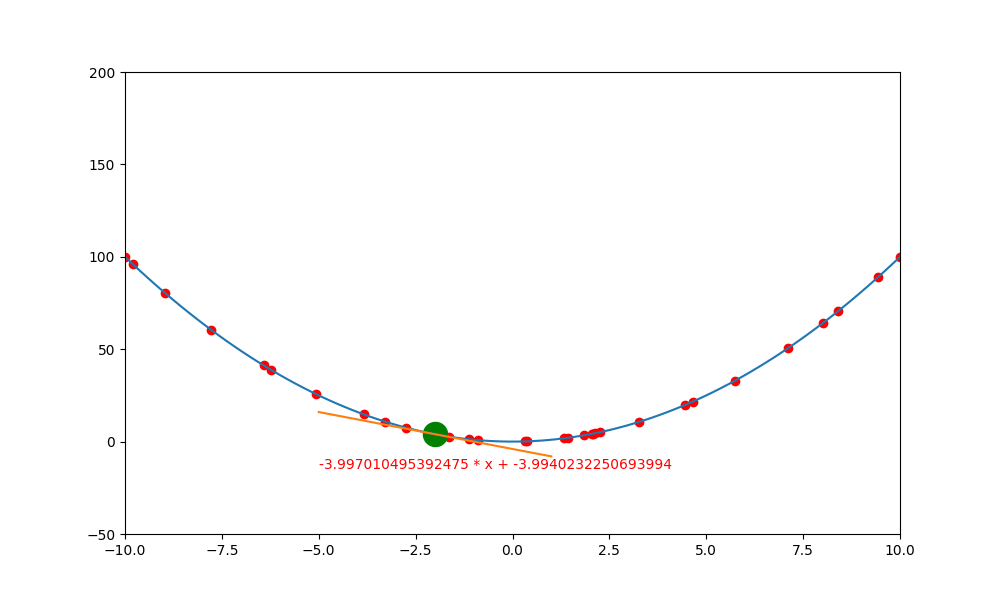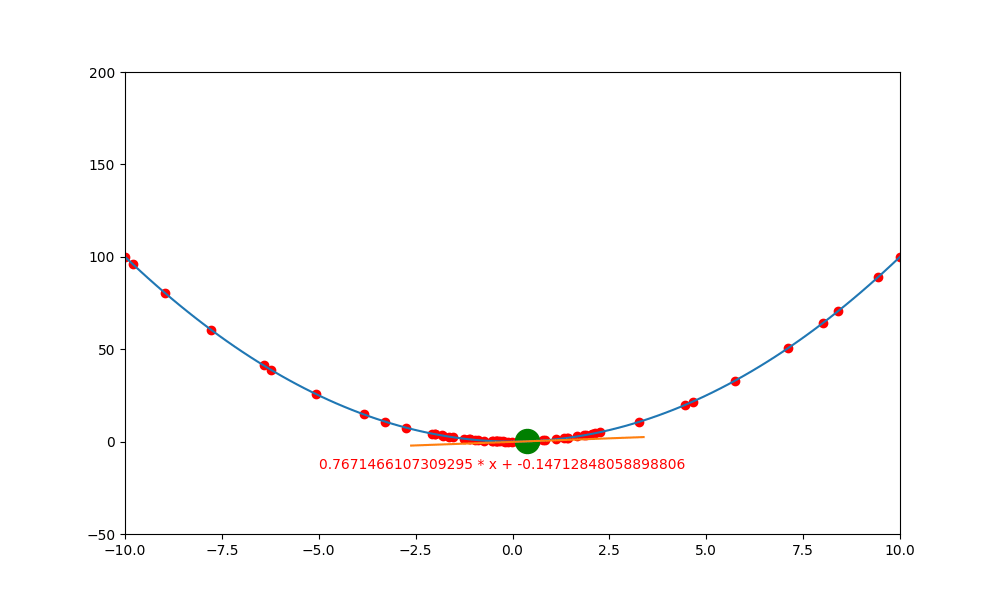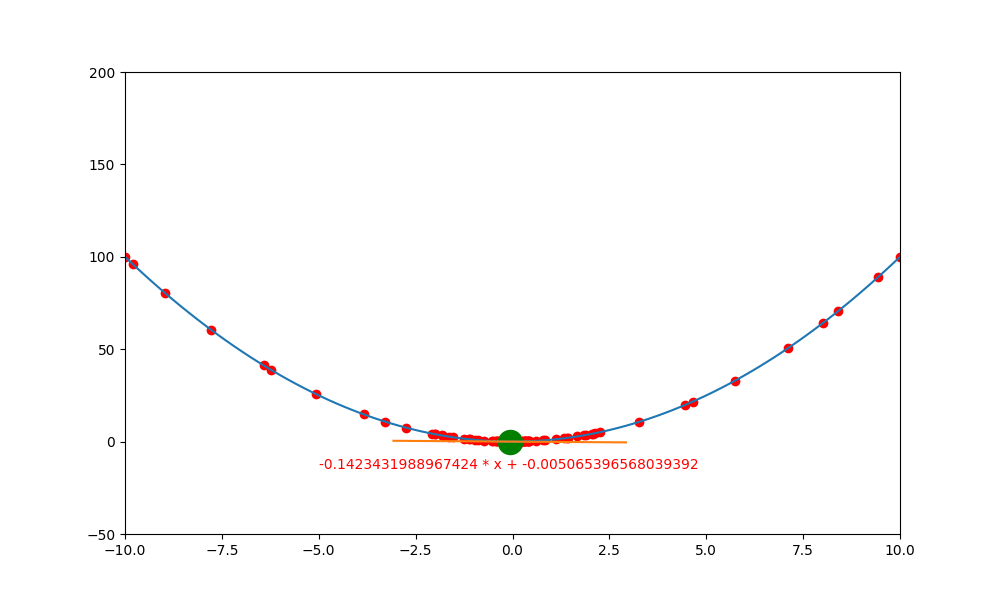
鞍點無動量
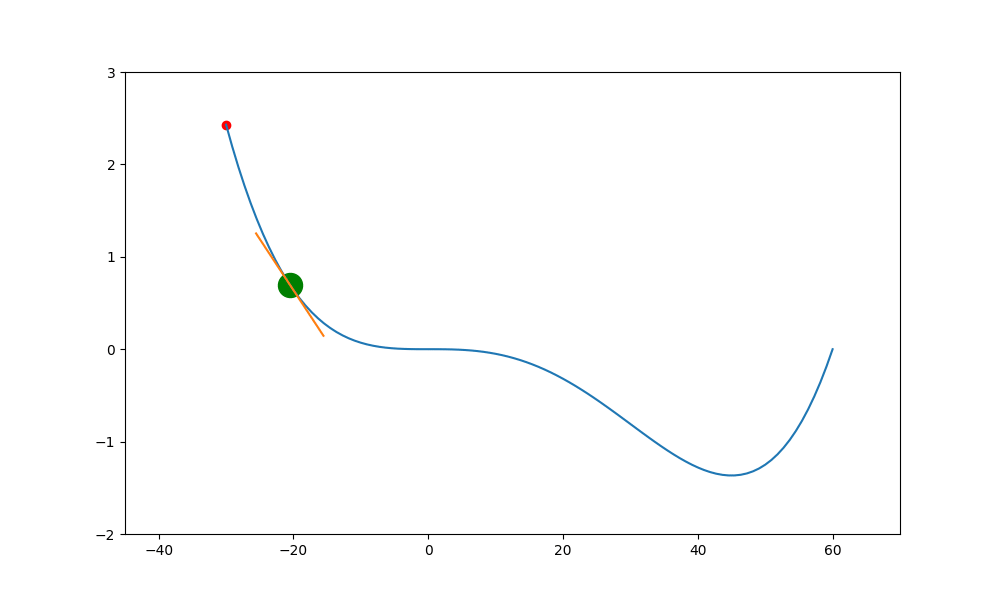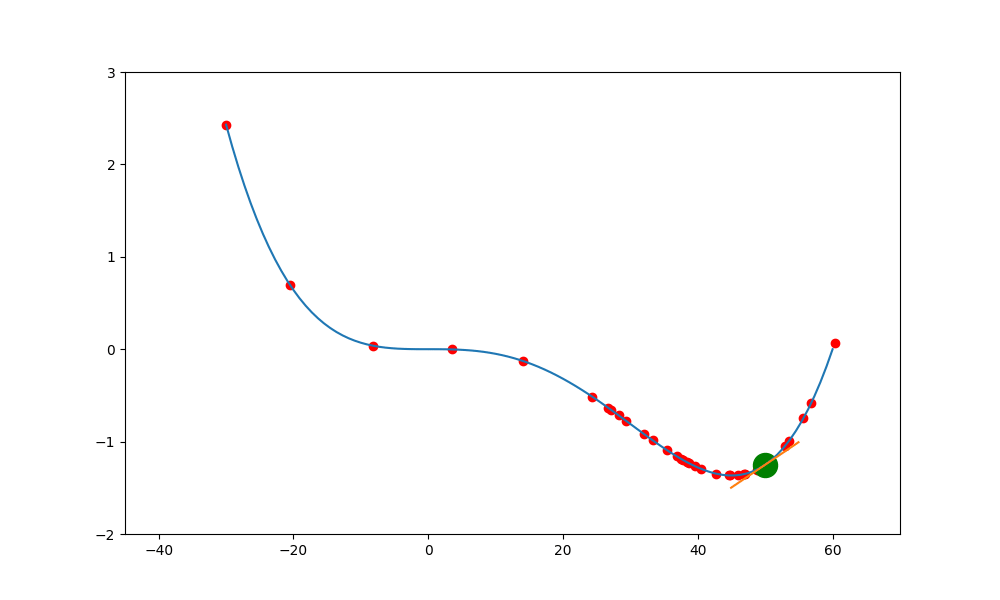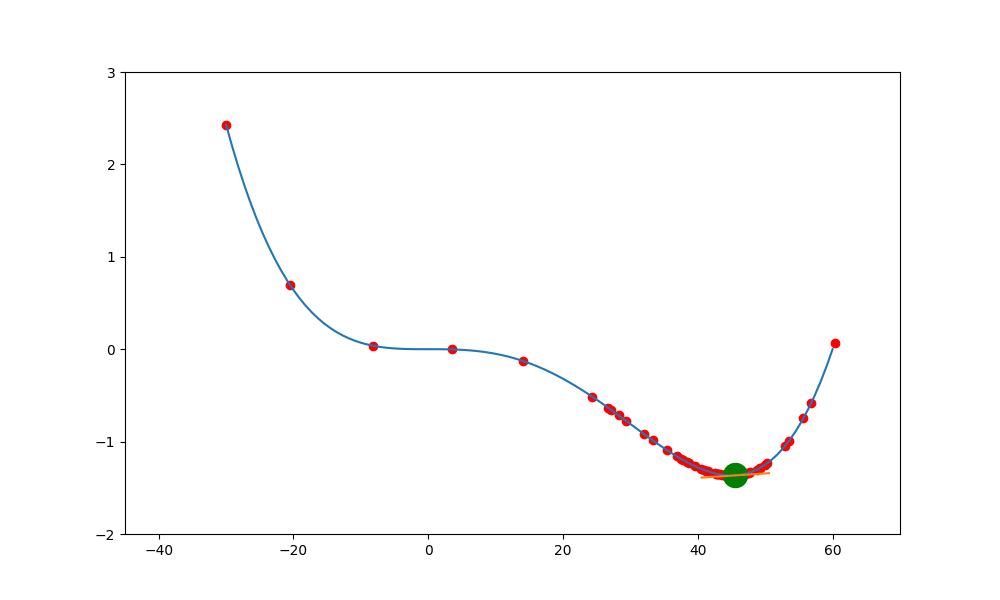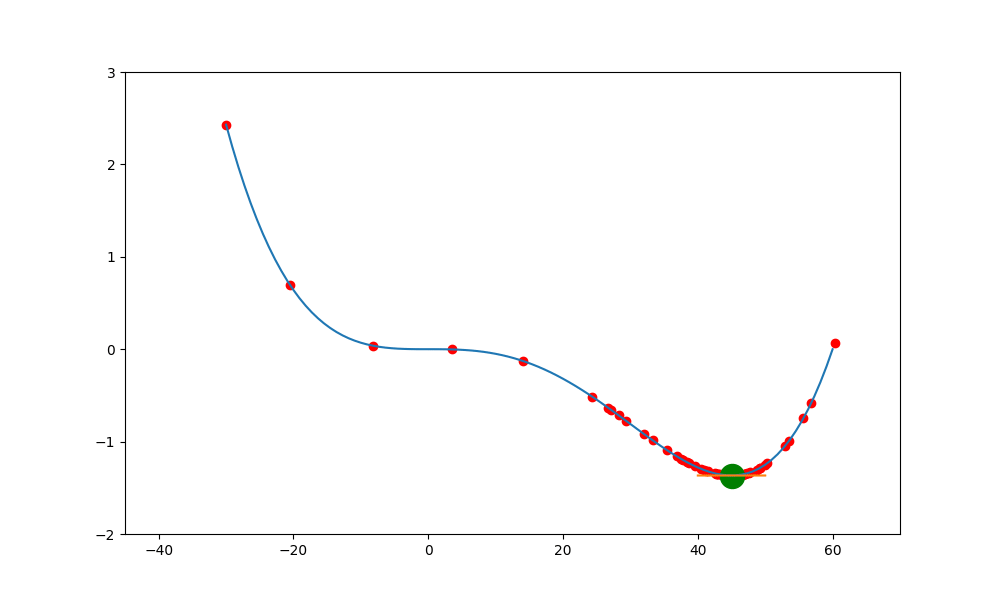
加入動量的重要性如下。當一個函數有鞍點且使用傳統學習方式時,就會卡在局部最小值中,無法突破
import numpy as np
import pylab as plt
#y = x^4 - 60x^3 - x + 1
def f(x):
x=np.array(x)
#因值很大,所以除以 shrink 縮小 y 值
y=(np.power(x,4) - 60 * np.power(x,3) - x + 1) / shrink
return y
def df(x):
return (4*np.power(x,3) - 180 * np.power(x,2) -1 ) / shrink
def bias(a, x):
return f(x)- a * x
shrink = 1e6
x=np.linspace(-30,60,100)
y=f(x)
current_x = x[00]
traces=[current_x]
plt.figure(figsize=(9,6))
ax=plt.axes()
epochs=60
lr=35
for i in range(epochs):
ax.clear()
ax.set_xlim(-45, 70)
ax.set_ylim(-2, 3)
ax.plot(x, y, c='b')
#偏微分
a = df(current_x)
b = bias(a, current_x)
#畫導線
xl=current_x-3
xr=current_x+3
yl = a * xl + b
yr = a * xr + b
ax.plot([xl, xr], [yl, yr], c='orange')
ax.scatter(traces, f(traces), c='r')
ax.scatter(current_x, f(current_x), c='g', s=200)
current_x -= a * lr
traces.append(current_x)
plt.pause(0.01)
plt.show()

上述就是使用傳統的方式,結果會卡在局部的低值(0,0) 中。
鞍點加動量
加入動量就可能突破鞍點,底下的圖就是加入球的慣性,讓球能越過下一波的高點,但這高點不能高於上一波的高點,否則會因動能不足而跨不過去。
import numpy as np
import pylab as plt
#y = x^4 - 60x^3 - x + 1
def f(x):
x=np.array(x)
#因值很大,所以除以 shrink 縮小 y 值
y=(np.power(x,4) - 60 * np.power(x,3) - x + 1) / shrink
return y
def df(x):
return (4*np.power(x,3) - 180 * np.power(x,2) -1 ) / shrink
def bias(a, x):
return f(x)- a * x
shrink = 1e6
x=np.linspace(-30,60,100)
y=f(x)
current_x = x[00]
traces=[current_x]
plt.figure(figsize=(9,6))
ax=plt.axes()
epochs=60
lr=35
v = 0
mu = 0.9
for i in range(epochs):
ax.clear()
ax.set_xlim(-45,70)
ax.set_ylim(-2,3)
ax.plot(x,y, c='b')
a=df(current_x)
b=bias(a, current_x)
xl = current_x - 3
xr = current_x + 3
yl = a * xl + b
yr = a * xr + b
ax.plot([xl, xr], [yl, yr], c='orange')
ax.scatter(traces, f(traces), c='r')
ax.scatter(current_x, f(current_x), c='g', s=200)
ax.text(-10, -1.5, f'{a:.7f} * x + {b:.7f}', color='red')
#計算下一點
v = a * lr + mu * v
current_x -= v
traces.append(current_x)
plt.pause(0.01)
plt.show()